After reading this article you will be able to fix some of the problems that stop a user from using their external USB hard disk drives properly & will also help in the situation where your Windows Operating system based computer does not detect your external Hard disk drive.
There are quite a few explanations for this problem & I have compiled this guide to address almost all of the known issues & help a user get rid of these problems for a smoother computing experience.
This guide addresses the most basic & the complex procedures to resolve some problems with your external hard disk drive. Follow the steps below:
Checking USB Connection
- If you External drive is USB powered, make sure that your cable is connected properly and the USB slot is a powered slot.
- Try replacing the USB Cable
- If your external drive is powered through an adapter, make sure your adapter is working fine, replace and check, if necessary.
- Try plugging your drive into another USB port
USB Drivers
- Always make sure that you have the latest USB & Chipset drivers installed in your computer.
- To check, run windows update to update your computer
- or
- Go to your motherboard / system manufacturer’s support website, download & install the latest drivers from there.
Device Management
- If you plug-in your device & it does not show up in my computer. The first thing to check is that whether your device has been detected in your computer or not.
- To check
- Go to start menu & type Device Manager
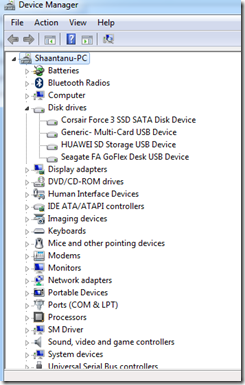
- Now, there are two things to check here. The first thing is whether your device is listed within disk drives of not. Check the screenshot above to confirm that my Seagate Go Flex USB device is listed there. In a similar way, you external USB device should be listed here.
- Just to make sure click the last button, just under Help menu, to refresh the hardware listed there & to install any newly added device.
- Second, thing to check is your Universal Serial Bus Controllers, list therein ( device manager ) & make sure all USB ports and enabled and are working properly.
Now,
- Go to start menu and type device management or right click the computer icon and click on device management ( you might have to provide administrator password here )
- Double click on storage
- Double Click on Disk Management
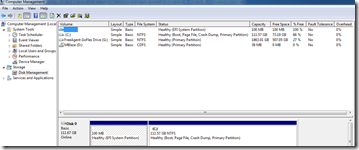
- Refer the screenshot above and make sure all of your drives listed here have a drive letter assigned to them,
- if you see a drive that does not has a drive letter assigned to them
- Right Click that drive
- Click on Change Drive letters & paths
- Now, add a drive letter here.
Running Disk Diagnostics
- Sometimes due to a error in file system or on the disk, your hard disk might just fail to detect in your computer system.
- An easy way is to gain access to a diagnostic software that might be available free to you on the hard disk manufacturer’s website.
- Download & install such software.
- Run the software to detect issues with your drive
Using a Live Disk, just to check
- If you have any live disk with you, you can boot from that disk to check if it detects external drive.
- Gparted live CD is a good tool to start with
- If a Live CD detects your drive, it’s time to repair your Windows installation.
- Check your disk for errors before exiting the live CD
Repairing Windows File System
- If you have a Windows CD / DVD with you or if you have a Windows 7 repair disc, boot from it
- On the first menu press Shift + F10
- This will open up the command prompt
- type diskpart
- type list disk
- If you see your external disk here
- type select disk n ( n being the no. example 0 , 1 ,2 listed besides your disk )
- if everything seems fine here ( size, file system etc. )
- type exit
- type exit again
- Run CHKDSK with the drive letter
- Boot back into Windows
- Go to, Run ( Windows key + R )
- Type, SFC /SCANNOW
- wait for the process to complete
IF this does not solve your problem
- check if you can open up your external enclosure
- Take your drive out and plug it directly into your computer system
- If your drive works, backup your data
- Buy another External enclosure
- Plugin your drive to check if it works
- Make sure you backup your data before doing any of this.
- Format your drive ( repartitioning is also recommended )
- NOTE: Do any of the above said steps at your own risk. Do not open your computer hardware or your HDD external enclosure, if you are not comfortable with it. Hire a professional to do it instead. If any damage or warranty violations occur, the author of this article will not be held responsible for it.

Comments
71 responses to “Fix : External USB Hard Disk drive not detecting / not working properly problem in Windows 8 , 7 , Vista & XP”